今回は音程についてのお話をしていこうと思います。
まず、基本的なところから説明していきたいと思います。
- ビブラートの練習曲。歌うまへの第一歩を踏み出そう！
- 作曲初心者も必見！定番のコード進行まとめ
- 高音が気持ちいい名曲。魅惑のハイトーンボイス
- 【初心者向け】ピアノで弾こう！カノン進行を使った曲まとめ
- コードでピアノ弾き語りに挑戦したい方必見！懐メロ～最新曲まで一挙紹介
- エレキベース初心者のための練習曲
- 初心者にオススメのバンドスコアまとめ。簡単な曲を紹介
- 【挑戦】高音メロ・ハイトーンボイスなアニソンまとめ
- 【練習！】春休みのベース初心者のための練習曲
- 【初心者】まずはこの曲から！ジャズ初心者のための練習曲まとめ
- 【高音注意！】歌うのが難しい高い曲
- 【ギター】コード進行が簡単！弾き語りにオススメな邦楽まとめ
- スローテンポで歌いやすい曲。音域やリズムにも注目！
- 日本の哀歌に込められた魂の叫び。心に響く至極の名曲を紐解く
- ストリートダンス初心者必見。各ジャンルの基本ステップまとめ
- 「お」から始まるタイトルの曲【カラオケ＆しりとりにも！】
- 【童謡】ピアノ初心者でも簡単に弾ける！シンプルなコードの曲を紹介
- 【作曲】定番コード進行を使っている有名曲まとめ【耳コピ】
- 難易度S級!?音域が広い曲まとめ
そもそも音程って何だろう？
http://o-dan.net/ja/
皆さんはカラオケに行くこともあるとは思います。
その際に採点機能を使ったことがありますか？
その採点機能を使うと「音程が正確ですね」や「少し音程が下がり気味です」などさまざまなコメントが返ってくると思います。
ここでの「音程」という言葉の意味は音の高低、すなわちピッチ（pitch）のことをいいます。
しかし音楽における「音程」という言葉の意味は、「2つの音の隔たり（距離）」のことをいいます。
例えばドからミはどれぐらいの距離なのか、ファからドはどれくらいの距離なのか。
それを表すものが「音程」になります。
音程にも単位がある
私たちが日常で使う距離を表す単位、m（メートル）、km（キロメートル）があるように、音程にも単位が存在します。
音程には「度」を用いて、2度、4度、7度というように表します。
基本的には1～8度を使うことが多く9度以上の音程を複音程（ふくおんてい）といいます。
なので、テンションにあたる9th、11th、13thは複音程にあたります。
音程の種類
音程を表すときに使われるのが「全音」と「半音」です。
半音は音程の最小単位であり、全音は半音2つ分です。
この2つを使って音程を表していきます。
そして音程には度数だけではなく「長」「短」「完全」を使って、長3度、完全5度、短6度などと表します。
1度
1度はユニゾンとも呼ばれ2つの音が同じ音になります。
したがって、1度には半音も全音も含まれていません。
1度は「完全1度」と表し長1度、短1度などは存在しません。
2度
2度は2種類あります。
半音が2つ、すなわち全音が含まれていたら「長2度」、半音が1つのときは「短2度」といいます。
3度
3度にも2種類あり、半音が4つ、すなわち全音が2つ含まれていたら「長3度」、半音1つと全音1つが含まれていたら「短3度」といいます。
4度
4度は半音が1つ、全音が2つ含まれていたら「完全4度」といいます。
こちらは1度と同じく、長4度、短4度は存在しません。
5度
5度は半音が1つ、全音が3つ含まれていたら「完全5度」といいます。
こちらも長5度、短5度は存在しません。
6度
6度は2種類あり、半音が1つ、全音が4つ含まれていたら「長6度」、全音が4つ含まれていたら「短6度」といいます。
7度
7度も2種類あり、半音が1つ、全音が5つ含まれていたら「長7度」、全音が5つ含まれていたら「短7度」といいます。
8度
8度はオクターブといわれており、「完全8度」といいます。
こちらには長8度、短8度は存在しません。
音程の変化
音程には増音程、減音程というものがあり、基本的には臨時記号を用いなければでてきません。
3度を使ってみてみましょう。
こちらは長3度ですが、ここでミに♯を付けます。
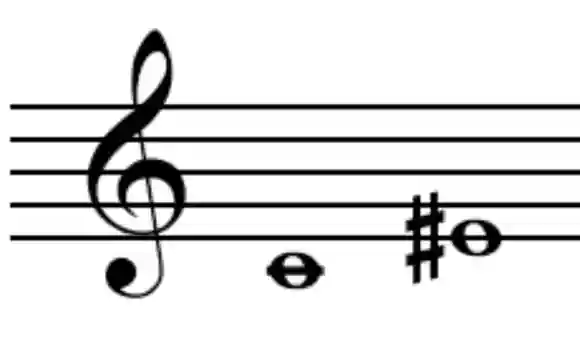
♯を付けたことによってさらに半音が1つ増えました。
これを「増3度」といいます。
次にミに♭を付けてみます。
フラットを付けたことによって半音が1つ減りました。
半音＋全音なので「短3度」になります。
ここでミに♭♭を付けるとさらに半音が1つ減ります。
これを「減3度」といいます。
したがって、音程の変化にはこのような規則性があります。
減⇔短⇔長⇔増、の通りになります。
減音程からいきなり長音程、増音程にはなりません。
1つずつ段階を踏んで変化していきます。
完全音程の場合また規則性が変わります
5度を使ってみてみましょう。
画像は完全5度ですが、ソに♯をつけると半音が1つ増えるので「増5度」いいます。
ソに♭をつけると半音が1つ減るので「減5度」といいます。
この減5度は3つの全音で構成されているので「三全音（さんぜんおん）」または「トライトーン」といいます。
このトライトーンはあとでお話しすることに非常に深く関わってきます。
話が反れましたが完全音程の音程の変化には、減⇔完全⇔増となります。
終わりに
今回はいったんここで区切ります。
次回は音程をコードや楽器に関連付けてお話ししようと思います。
ライタープロフィール
キーボーディスト
佐々木祐
北海道札幌市出身。
19歳の時に専門学校に入学し、音楽理論などを2年間学ぶ。
キーボーディストとしても活動しております。
こちらの方で音楽理論の記事を作っていました。
ウェブサイト：http://mrpianoman0620.blogspot.jp
Twitter：sasasa_maegami