小学生向けの算数クイズ
小学生の算数、と言っても学年が上がるごとに難しくなり、最後は大人でもちょっとややこしく感じるような問題、登場しますよね。
しかしそれで「算数なんて嫌いだ」と思ってしまうのはもったいない。
ということでこの記事、算数があまり得意じゃないお子さんにもオススメなものをそろえています。
学校で習う計算式の問題とはちょっと違う、頭をひねって解いていくクイズ形式のものばかりなので、楽しく挑戦できるはずです。
もしかしたら苦手意識もなくなるかも。
頭の体操の一貫として、親子でチャレンジしてみるのもありですよ。
小学生向けの算数クイズ（1〜10）
楽しい勉強ドリル問題集
新1年生にオススメの足し算と引き算の問題です。
ドリルのように問題がたくさんあるので、何問も挑戦して足し算や引き算に慣れたいという小学生はぜひ解いてみてくださいね！
この問題集は「1+2+1=4」のように、基本的に3つの数字を足し引きして10までの答えになります。
1〜10の数字の概念がわかっていれば挑戦できますよ。
0を足したり、引き算をしてから足し算をするなど、バリエーションも豊富！
算数が得意な子は、お友達とどちらが早く答えられるかを競い合っても楽しそうですね！
簡単そうで意外と解けない図形
小学生4年生なら解ける!図形の周の長さを求める問題です。
ただの長方形なら縦と横の長さをすべて足せば答えが出ますが、この問題は長方形の一部がデコボコしていて、長さがわからないところがありますね。
一見とても難しそうに見えるこの問題ですが、わからない部分のパーツを繋いでみてください。
そうすれば、わかっている部分と同じ長さになりますよね。
足し算の知識とひらめきがあれば、算数が得意な低学年の子でも解けるかもしれませんね！
アジは何匹？
小学生3年生の算数の知識があれば解ける問題です。
しかし同時に、算数オリンピックにて出題され正答率が20%に満たなかった超難問でもあります！
あなたは魚屋さんでいろいろな魚を買いお金を支払います。
支払った金額とそれぞれの魚の値段はわかっていますが、どの魚を何匹買ったのかはわかりません。
この状態で、ある一つの魚を何匹買ったのかを求めるのがこの問題です。
問題だけ見ればすぐに答えがわかりそうなものですが、これがなかなか難しい！
あなたの算数と知識とセンスをいかして、ぜひ解いてみてくださいね！
【算数パズル】迷路の問題全3問
迷路が好きな小学生にオススメの算数クイズです！
この問題はスタートからゴールまでが迷路のようになっていて、「一度通った道は通れない」「扉は一回しか開けられない」など、決められたルールを守りながらゴールにたどり着く、またはゴールがどこかを当てるクイズ。
文字や数字の問題とは違い、頭で考えながら視覚的に進められるので、お友達と何人かで集まって一緒に解くと盛り上がりますよ！
ルールをよく読んで、正しいルートを導き出しましょう！
中学入試では基本事項のありがちな図形問題
算数の授業でも頻繁に登場する正統派の図形問題。
縦の長さが10cmの長方形の中に扇形が2つ重なっており、2つの扇形以外の面積をア、2つの扇形が重なっている部分をイとし、アとイは同じ面積とのこと。
扇形の面積の求め方、長方形の面積の求め方を知っていれば、あとはどう計算式を組み立てていくかが正解への鍵ですね。
図形問題は面積を求める公式だけでなく、考え方が試されますのでとにかく数をこなすのがポイントでしょう！
面積の総和
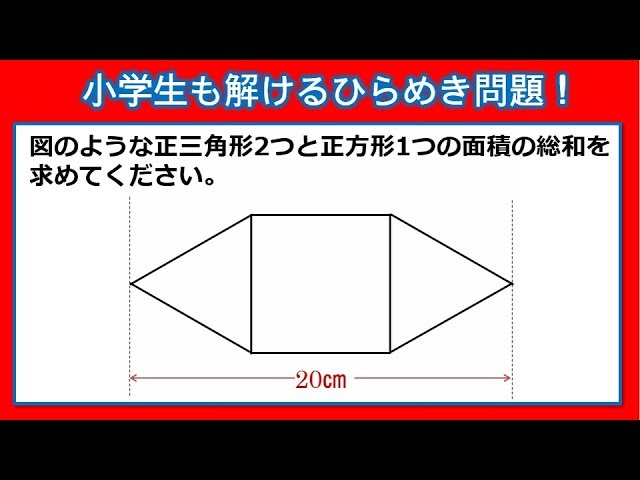
2つの正三角形と1つの正方形の面積の合計を求める問題です！
算数が苦手な小学生は、図形が複数になるとそれだけで「わからない」と思ってしまいますよね。
けれど少しだけ苦手意識を落ち着けて、わかる部分の長さを考えていきましょう。
この問題でまず注目するべき点は、正三角形と正方形の組み合わせなので、すべての辺の長さは同じだということですね。
補助線なども活用して、まずは正三角形の高さと底辺の半分の長さを考えていきましょう！
発想力が試されるパズル！
このクイズは、頭のひらめきが試されるパズルです。
一見なんのマークかわからない謎のマークが3×3の9マスのうちの8マスに描かれています。
右下の1マスだけが空欄になっていて、そこにはどんなマークが入るかを答える問題。
ハートマークや丸や三角を組み合わせたもの、ローマ字のMのようなものなどさまざまでパッと見ただけでは法則がわかりませんが……。
じっくりと見ているとあることに気付くはず！
ヒントは、それぞれの図形やMを組み合わせたものと見ないこと、マスが全部で9つあることです。